数学奇趣：奇函数与偶函数相乘，结果竟是……

在数学的世界里，函数以其独特的形态和性质，为我们揭示了自然界和人工系统中纷繁复杂的规律。其中，奇函数和偶函数作为两种基本的函数类型，不仅在数学分析中占有重要地位，而且在实际应用中也有着广泛的应用。那么，当奇函数与偶函数相遇，它们相乘的结果又会是什么呢？

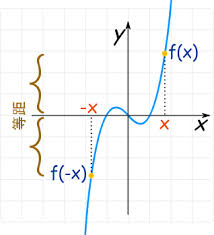
首先，我们来回顾一下奇函数和偶函数的定义。如果一个函数f(x)满足f(-x)=-f(x)，那么我们就称这个函数为奇函数。奇函数关于原点对称，其图像在坐标平面上是一个以原点为中心的点对称图形。相反，如果一个函数g(x)满足g(-x)=g(x)，那么我们就称这个函数为偶函数。偶函数关于y轴对称，其图像在坐标平面上是一个以y轴为中心的轴对称图形。

现在，我们考虑一个奇函数f(x)和一个偶函数g(x)的乘积h(x)=f(x)g(x)。为了探究h(x)的性质，我们可以计算h(-x)：

h(-x) = f(-x)g(-x)

由于f(x)是奇函数，所以f(-x)=-f(x)；而g(x)是偶函数，所以g(-x)=g(x)。将这两个性质代入上式，我们得到：

h(-x) = -f(x)g(x) = -h(x)

由此可见，h(x)满足奇函数的定义，即h(-x)=-h(x)。因此，我们可以得出结论：奇函数乘以偶函数的结果是一个奇函数。

这个结论在数学分析中有着重要的意义。它不仅为我们提供了一种判断函数奇偶性的新方法，而且还在函数的性质研究、方程的求解以及不等式的证明等方面发挥着重要作用。同时，这个结论也为我们理解自然界和人工系统中的某些现象提供了新的视角和工具。

然而，需要注意的是，虽然奇函数乘以偶函数的结果是一个奇函数，但这并不意味着所有具有奇偶性的函数都可以通过这种方法来构造。事实上，函数的奇偶性只是函数性质的一个方面，要全面理解和分析一个函数，我们还需要考虑其单调性、周期性、有界性等其他性质。

总之，奇函数乘以偶函数等于奇函数，这是数学中一个有趣而重要的结论。它不仅丰富了我们对函数奇偶性的认识，而且为我们解决实际问题提供了新的思路和方法。在未来的学习和研究中，让我们继续探索数学的奥秘，发现更多有趣而有用的结论。